こんにちは

STORYの石川です

僕は今独学で統計学を勉強しているのですが、

本やサイトではnやらΣやらeなど複雑な数式で説明がされ

素晴らしいほどアホな高校に通っていた僕ではなかなか頭に入ってこず、

勉強があまり進みませんでした。

もっと簡単に説明してくれたらいいのに、、、、

その思いや、自分の復習の意味も込めて、このブログで実は簡単！！という雰囲気が伝わればいい

3分クッキングのような統計学の話をしていけたらと思います。

今回は統計学の基礎、である「平均」や「中央値」といった部分(基本統計量)について書いていきます。

■平均値

こちらは普段皆さん使ってると思います。

全部足して、足した数で割った数値です。

■中央値

中央値は「データを小さい順に並べて、ちょうど中央にある数値」のことです。

[2,3,5,7,8]　→　こちらの中央値は5です。

データが偶数の場合はちょうど中央にくるデータ２つの平均値です。

[2,3,5,7,8,10]　→　こちらの中央値は5と7の平均である6です。

■分散

分散は「データがどの程度平均値の周りにばらついているか」を表す指標です。

ばらつき？？となると思うのですが、

例えば[2,3,5,7,8]のデータがあったとします。

このデータの平均値は5となり

それぞれのデータが平均からどれだけ離れているかを可視化しようとすると下記の表になります。

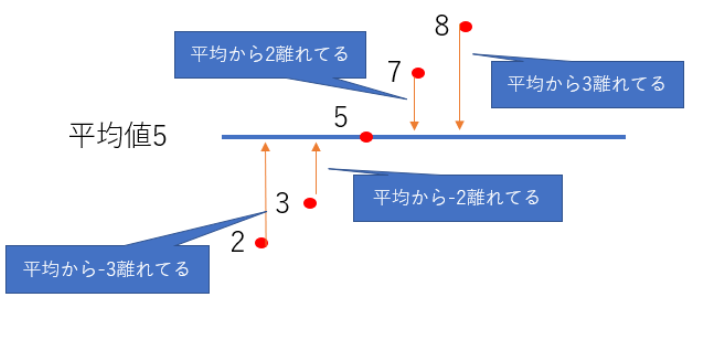
この離れている数字を二乗して足して平均を出した数字が分散となります。

なのでこちらの分散は、((-3)2+(-2)2+(0)2+(2)2+(3)2)/5=5.2になります。

なぜ二乗するかというと、そのまま足し合わせたら

-3+-2+0+2+3=0になってしまいます

マイナスを消したいから二乗するのです！

■標準偏差

標準偏差は分散の平方根をとったものを言います。

なぜわざわざ平方根を取るのかというと

先程の分散でマイナスを取るために二乗したため、数字の単位は元のデータの単位と異なってしまいます。

例えば、魚の体長データがcmで記されていたとすると

二乗したため、分散の単位はcm2となってしまいます。

これでは一匹あたり平均何cmばらついているのかと言えなくなってしまうため

平方根をとり単位を元のデータと揃える必要があるのです。

どうでしたでしょうか？

なんとなくホワーンとでも理解していただけたら嬉しいです。

僕も改めて自分の言葉で書くと復習になるので

定期的にこのシリーズを書いていけたらと思います

ではまた！